前幾天做的都是回歸問題的模型,而今天我們做二元分類問題時,就要和大家介紹邏輯回歸 ( Logistic Regression ) 這個模型,我們要讓模型根據輸入的年齡、體重、血糖、性別這些特徵,來預測是否患有糖尿病,這是個二元分類問題,用來分類「患有糖尿病 ( 模型輸出 1 )」和「沒有患有糖尿病 ( 模型輸出 0 )」這兩類。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
https://drive.google.com/file/d/1T1ByLWTmvMTNUSldTev24tRjTJYxtvKp/view?usp=drive_link
設定之後陣列輸出的格式與讀取資料 ( 上方連結 ):
np.set_printoptions(formatter={"float": "{: .2e}".format})
data = pd.read_csv("Diabetes_Data.csv")
對 Gender 欄位做獨熱編碼 OneHot Encoding:
data["Gender"] = data["Gender"].map({"男生": 1, "女生": 0})
提取出資料的特徵 ( 包含四個 ) x 和標籤 y 再對資料集做切割,一樣是切割 80% 資料做訓練剩下做測試,並且對訓練資料做特徵縮放:
x = data[["Age", "Weight", "BloodSugar", "Gender"]] # Feature
y = data["Diabetes"] # Label
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=87) # 資料切割
x_train = x_train.to_numpy()
x_test = x_test.to_numpy()
scaler = StandardScaler() # 特徵縮放正規化
scaler.fit(x_train) # 訓練資料擬和
x_train = scaler.transform(x_train)
x_test = scaler.transform(x_test)
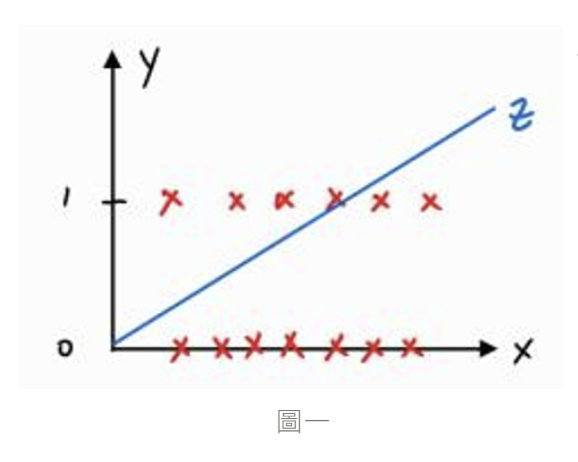
因為二元分類問題屬於邏輯回歸問題,所以資料標籤不是 0 就是 1,而這時我們用線性回歸的方式來設計模型就顯得不妥 ( 下圖一 ),我們應該要讓模型預測出來的結果值範圍鎖在 0 - 1 之間,可以把 0 與 1 想成是患糖尿病的機率 0% 與 100%,如果模型預測出來的是 0.9,就表示預測結果就是有 90% 機率患糖尿病,而我們目前的模型為線性模型 ,要怎麼讓這函數輸出範圍介於 0 - 1 ? 所以就會用到 Sigmoid Function,是一種 Activation Function,而我們只要把
( model ) 當作輸入丟進這個函數中,它就會讓輸出的值鎖定在 0 - 1 之間 ( 下圖二 )
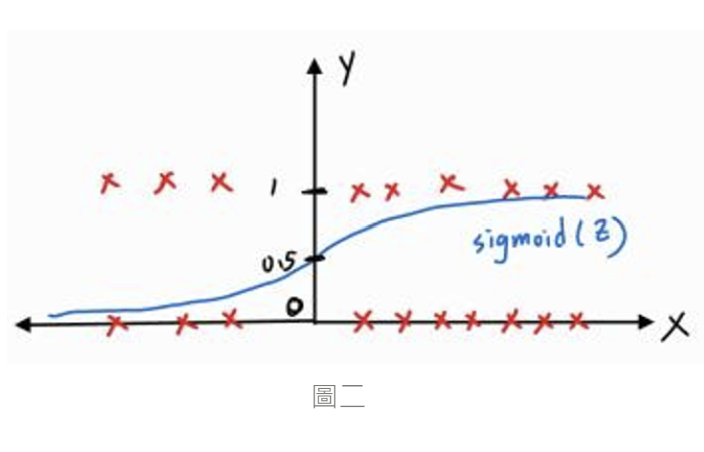
Sigmoid 函數實作,而把線性模型 z 傳入 Sigmoid 後就會得到新的模型 y_pred
def sigmoid(z): # Input: Linear Model z
return 1 / (1 + np.exp(-z))
y_pred = sigmoid(z)
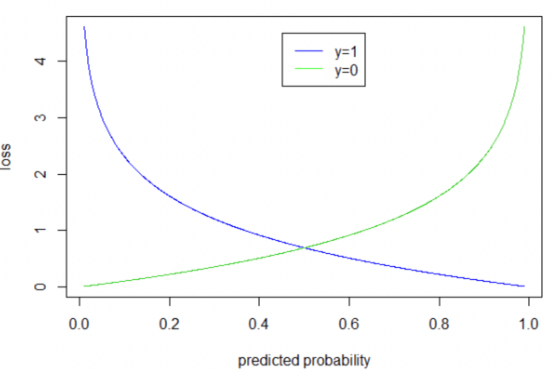
在成本函數上,線性回歸是用最小平方法來實現,目的是為了讓預測結果去擬和真實資料,而邏輯回歸是採二元交叉熵 ( Binary Cross Entropy,BCE ) 的方法,對於預測結果來說,其目的並不是以接近真實資料為目標去做擬和,差別是在在計算成本上前者是取預測結果和真實資料間的距離,後者則是代入到 BCE 的公式中去計算該成本,成本大小和真實資料之間的距離較無關係,值得注意的是可以把 BCE 這著函數看成由兩個函數 ( 藍色和綠色 ) 組成;在使用上,我們把 model 傳入 BCE,因為 model 預測的結果為機率 ( 介於 0 - 1 ),所以 BCE 我們可以 focus 在 [ 0 , 1 ] 區間即可 ,可以想如果當真實資料為 1 ( = 1 ) 時將模型預測
套用藍色函數,此時 model 預測的值越接近 1,模型損失就越小,而越接近 0 模型損失越大,而在
= 0 時套用到綠色函數,預測值越接近 0 損失就會越小反之亦然,如此一來就可以透過真實資料的邏輯狀態 1 OR 0 去計算成本大小,因此我們可以得到 BCE 公式:
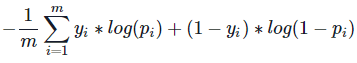
def cost(x, y, w, b): # x:feature y:label
z = (w * x).sum(axis = 1) + b
y_pred = sigmoid(z)
cost = -y * np.log(y_pred) - (1 - y) * np.log(1 - y_pred) # Binary Cross Entropy
return cost.mean() # 取平均值
def gradient(w, b):
z = (x_train * w).sum(axis=1) + b
y_pred = sigmoid(z) # 經過 sigmoid 後的 model
w_gradient = np.zeros(x_train.shape[1])
b_gradient = (-2 * (y_train - y_pred)).mean()
for i in range(x_train.shape[1]):
w_gradient[i] = (-2 * x_train[:, i] * (y_train - y_pred)).mean()
return w_gradient, b_gradient
gradient(w, b)
這裡我們用梯度下降優化模型並用訓練資料得到最佳解 w_final、b_final:
def gradient_descent(x, y, w_init, b_init, learning_rate, cost_func, gradient_func, run_iter, per_iter=1000):
w = w_init
b = b_init
w_hist = []
b_hist = []
cost_hist = []
for i in range(run_iter):
w_gradient, b_gradient = gradient_func(w, b)
w_step = - learning_rate * w_gradient
b_step = - learning_rate * b_gradient
w = w + w_step
b = b + b_step
w_hist.append(w)
b_hist.append(b)
cost_hist.append(cost_func(x, y, w, b))
if(i % per_iter == 0):
print(f"time{i:5}, cost:{cost_func(x, y, w, b): .4e}, w:{w}, b:{b: .2e}")
return w, b, w_hist, b_hist, cost_hist
# 初始參數
w_init = [1, 2, 3, 4]
b_init = 1
# 學習率
learning_rate = 1.0e-2
# 迭代次數
run_iter = 10000
w_final, b_final, w_hist, b_hist, cost_hist = gradient_descent(x_train, y_train, w_init, b_init, learning_rate, cost, gradient, run_iter)
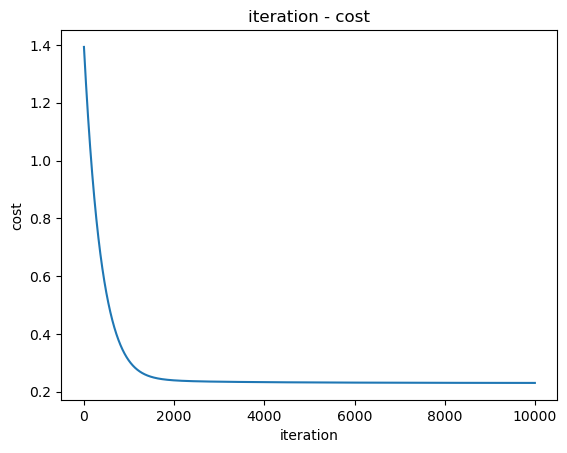
plt.plot(range(10000), cost_hist[:10000])
plt.title("iteration - cost")
plt.xlabel("iteration")
plt.ylabel("cost")
plt.show()
把找到的最佳參數放進 model 後跑測試特徵資料,會得到對於每筆資料預測出來的機率,因此我們就可劃分為 1 和 0 兩類 ( 患 / 沒患糖尿病 ),只要預測機率 > 0.5 都歸類為 1,< 0.5 的都歸到 0,最後在和測試標籤資料比對 ( y_pred == y_test ),比對結果會是布林值陣列,陣列中有幾個 True 就代表有幾筆資料預測正確,就可以知道 model 的準確率
z = (w_final * x_test).sum(axis=1) + b_final
y_pred = sigmoid(z)
y_pred = np.where(y_pred > 0.5, 1, 0)
acc = (y_pred == y_test).sum() / len(y_test) * 100
print(f"accuracy: {acc}%")
在今天我們學到:
那我們下篇文章見 ~
https://www.youtube.com/watch?v=wm9yR1VspPs
GrandmaCan-我阿嬤都會 - 機器學習課程
